solving one step equations pdf

Understanding One-Step Equations

One-step equations are the simplest form of algebraic equations. They require only one operation to solve.The goal is to isolate the variable.

Definition and Basic Principles

One-step equations are the simplest equations around. They are the stepping stone from basic math to algebra. They require one operation, be it adding, subtracting, multiplying, or dividing, to arrive at the solution. The main objective is to have the variable (x or any other letter) alone on one side of the equation. The variable must be isolated to solve the equations. In essence, you’re undoing the operation that’s affecting the variable. For example, if you have x + 5 = 12, you would subtract 5 from both sides to isolate x. Similarly, if you have 3x = 15, you would divide both sides by 3 to solve for x. Understanding this basic principle is crucial for tackling more complex algebraic problems later on. One-step equations are foundational to algebraic equations.

Solving One-Step Equations Using Addition

To solve, we need to isolate the variable by performing the inverse operation. With addition, we subtract from both sides to solve.

Isolating the Variable with Addition

Solving one-step equations using addition involves isolating the variable by using the inverse operation: subtraction. The principle behind this method is based on the properties of equality. To maintain the balance of the equation, any operation performed on one side must also be performed on the other side. When the equation involves adding a constant to the variable (e.g., x + a = b), isolating ‘x’ requires subtracting ‘a’ from both sides of the equation. This action cancels out the addition on the side with the variable, leaving ‘x’ alone and providing its value. For example, to solve x + 5 = 12, subtract 5 from both sides, resulting in x = 7. This simple yet crucial step forms the foundation for solving more complex algebraic problems. Checking your answer by substituting the found value back into the original equation is vital to ensure accuracy and a solid understanding of the solution process. Always remember that the goal is to get the variable by itself on one side of the equation.

Solving One-Step Equations Using Subtraction

To solve one-step equations using subtraction, add the number being subtracted from the variable to both sides of the equation. This isolates the variable.

Isolating the Variable with Subtraction

Solving one-step equations using subtraction involves isolating the variable by performing the inverse operation, which is addition. The Subtraction Property of Equality states that for any real numbers a, b, and c, if a = b, then a ⎼ c = b ⏤ c. This means you can subtract the same value from both sides of an equation without changing its balance. To isolate the variable, add the number that’s being subtracted from the variable to both sides of the equation. For example, if you have the equation x ⏤ 5 = 12, you would add 5 to both sides to get x = 17. This process effectively cancels out the subtraction, leaving the variable alone on one side of the equation. Always remember to perform the same operation on both sides to maintain equality and accurately solve for the unknown variable. Practice with various examples to master this technique. Using subtraction is a fundamental skill in algebra.

Solving One-Step Equations Using Multiplication

Using multiplication is a key technique to isolate variables. It is the inverse operation of division. Understanding this is crucial for algebra.

Isolating the Variable with Multiplication

When solving one-step equations using multiplication, the primary goal is to isolate the variable on one side of the equation. This involves using the inverse operation of division, which is multiplication. If the variable is being divided by a number, you multiply both sides of the equation by that number to cancel out the division. This process ensures that the variable stands alone, revealing its value and solving the equation. For example, if you have the equation x/3 = 5, you would multiply both sides by 3 to get x = 15. Remember, whatever you do to one side of the equation, you must do to the other side to maintain the balance and equality. This principle is fundamental in solving any algebraic equation. Practice with various examples, including integers, fractions, and decimals, will solidify your understanding and skills in isolating variables through multiplication. Mastering this technique is crucial for success in more complex algebraic problems.

Solving One-Step Equations Using Division

To solve, divide both sides by the variable’s coefficient. This isolates the variable, revealing its value and solving the one-step equation.

Isolating the Variable with Division

Division is the inverse operation of multiplication. When solving one-step equations involving multiplication, division is the key to isolating the variable. If an equation presents a variable multiplied by a coefficient (e.g., 3x = 15), dividing both sides of the equation by that coefficient will undo the multiplication. This process effectively separates the variable onto one side of the equation and the result on the other side, thus revealing the solution. For example, in the equation 3x = 15, dividing both sides by 3 gives x = 5, as 15 ÷ 3 = 5. It’s crucial to remember to perform the division on both sides to maintain the equation’s balance. This principle applies regardless of whether the numbers are integers, fractions, or decimals. Understanding and applying this inverse operation enables students to confidently solve a wide range of one-step equations where division is required. Mastering this skill is fundamental for success in more complex algebraic problems later on. Practice is crucial.

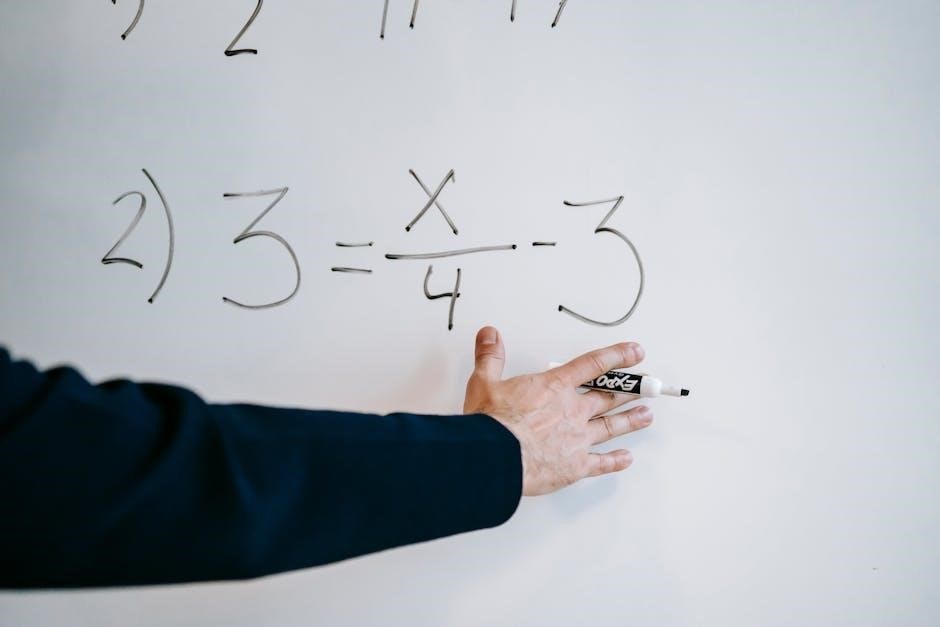
One-Step Equations with Integers

Working with integers introduces negative numbers into one-step equations. Apply the same inverse operations.

Practice with Positive and Negative Numbers

Solving one-step equations with integers involves practicing with both positive and negative numbers. The key is to remember the rules of integer arithmetic when applying inverse operations. For addition and subtraction, keep in mind that subtracting a negative number is the same as adding a positive number, and vice versa. For multiplication and division, remember that multiplying or dividing two numbers with the same sign results in a positive number, while multiplying or dividing two numbers with different signs results in a negative number. By practicing with a variety of problems involving positive and negative integers, students can develop a strong understanding of how to solve one-step equations regardless of the sign of the numbers involved. This skill is crucial for success in more advanced algebra topics, as it lays the foundation for solving more complex equations and working with algebraic expressions.

One-Step Equations with Fractions

One-step equations with fractions require applying inverse operations. Focus is on multiplying by reciprocals to isolate the variable effectively.

Solving Equations Involving Fractional Coefficients

When dealing with one-step equations that involve fractions, the primary goal remains isolating the variable. However, the presence of fractional coefficients requires a slightly different approach compared to equations with integer coefficients. The key technique here is to multiply both sides of the equation by the reciprocal of the fractional coefficient. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example, the reciprocal of 2/3 is 3/2. Multiplying a fraction by its reciprocal always results in 1, effectively canceling out the fractional coefficient and leaving the variable isolated. Consider an equation like (2/5)x = 8. To solve for x, we multiply both sides of the equation by the reciprocal of 2/5, which is 5/2. This gives us (5/2) * (2/5)x = 8 * (5/2). Simplifying, we get x = 20. Remember to simplify fractions before multiplying to make calculations easier. Also, be mindful of the signs when dealing with negative fractions. Applying these steps consistently will allow you to confidently solve one-step equations involving fractional coefficients.

Applications of One-Step Equations

One-step equations are fundamental in solving real-world problems. They translate simple scenarios into mathematical expressions.

Word Problems and Real-World Scenarios

One-step equations find applications in various real-world scenarios and word problems. These problems often involve translating a given situation into a mathematical equation and then solving for the unknown variable. For instance, consider a problem where you need to determine the original price of an item after a discount is applied. If the discounted price is $20, and the discount was $5, you can represent this situation with the equation x ⏤ 5 = 20, where x is the original price. Solving this one-step equation by adding 5 to both sides gives you x = 25, indicating that the original price of the item was $25. Similarly, if you know that three times a certain number equals 15, you can represent this with the equation 3x = 15. Solving for x by dividing both sides by 3 gives you x = 5, revealing the number to be 5. These examples demonstrate how one-step equations can be used to solve practical problems involving quantities, measurements, and relationships in everyday life, making them a valuable tool for problem-solving.